Участник проекта
Участник проекта
Участник проекта
Привет! Меня зовут Майя Трутнева.
Я ученица 8 класса МБОУ СОШ №1 г. Покров.
Играю на фортепиано, рисую, занимаюсь плаванием, участвую в математических олимпиадах, музыкальных конкурсах и конкурсах изобразительного искусства, а также в спортивных соревнованиях.
В сетевом проекте принимаю участие уже во 2-й раз. В этом году хочу превзойти свой прошлогодний результат :)
Всем участникам желаю удачи!
Привет! Меня зовут Майя Трутнева.
Я ученица 8 класса МБОУ СОШ №1 г. Покров.
Играю на фортепиано, рисую, занимаюсь плаванием, участвую в математических олимпиадах, музыкальных конкурсах и конкурсах изобразительного искусства, а также в спортивных соревнованиях.
В сетевом проекте принимаю участие уже во 2-й раз. В этом году хочу превзойти свой прошлогодний результат :)
Всем участникам желаю удачи!
Привет! Меня зовут Майя Трутнева.
Я ученица 8 класса МБОУ СОШ №1 г. Покров.
Играю на фортепиано, рисую, занимаюсь плаванием, участвую в математических олимпиадах, музыкальных конкурсах и конкурсах изобразительного искусства, а также в спортивных соревнованиях.
В сетевом проекте принимаю участие уже во 2-й раз. В этом году хочу превзойти свой прошлогодний результат :)
Всем участникам желаю удачи!

X региональный математический проект «Тайны натурального ряда чисел»
Страница участницы проекта Трутневой Майи
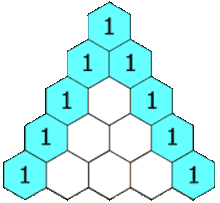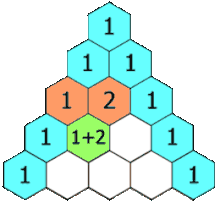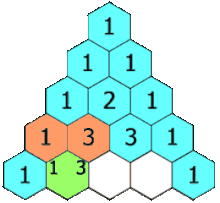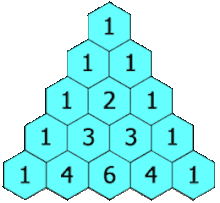
Треугольник Паскаля
Лента времени с указанием основных дат жизни,
вклада учёного в развитие математики, его изобретений.
Примеры различных вариантов изображения арифметического треугольника
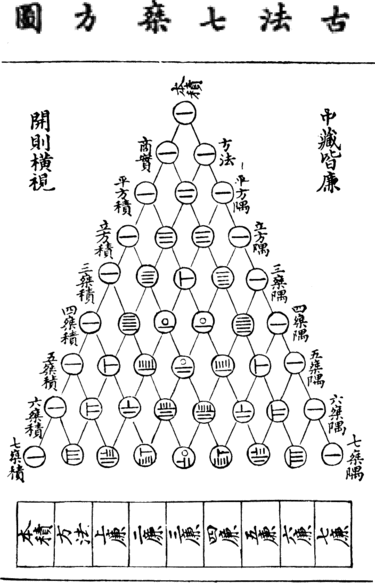 Ян Хуэй. Китайский средневековый манускрипт, «Ши Суо Суан Шу». | 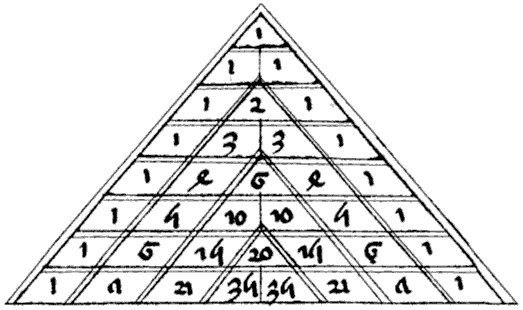 Омар Хайям |  Пингала, «Meru-Prastaara» |
|---|---|---|
 Никколо Тарталья. General Trattato di Numeri et Misure (общий трактат о числах и мерах), «Яшмовое зеркало четырех элементов» |  Паскаль, «Т�рактат об арифметическом треугольнике» |
Свойства, которыми обладает арифметический треугольник Паскаля

-
Второе число каждой строки соответствует её номеру.
-
Третье число каждой строки равно сумме номеров строк, ей предшествующих.
-
Треугольник Паскаля представляет собой различные системы измерения пространства: одномерное, двухмерное, трехмерное, четырехмерное и т.д.
-
Сумма чисел n-ной строки (отсчет ведется с нуля) треугольника Паскаля равна . Действительно, при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна .
-
Все строки треугольника Паскаля симметричны. Потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична.
-
Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего нас места, достаточно взглянуть на число, расположенное снизу и слева от последнего слагаемого (слева для правой диагонали, для левой диагонали будет справа).
-
Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный диагоналями, на пересечении которых находится этот элемент.
-
Если посчитать для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, то получится соответствующее число Фибоначчи.
-
Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно.
-
Первая диагональ треугольника Паскаля – это натуральные числа, идущие по порядку.
-
Вдоль второй диагонали треугольника выстроены треугольные числа (Треугольное число — это число кружков, которые могут быть расставлены в форме правильного треугольника. Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел) и их обобщения на случай пространств всех размерностей.
-
Третья диагональ треугольника Паскаля — это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).
-
Сумма чисел, стоящих на четных местах, равна сумме чисел, стоящих на нечетных местах.
-
Каждое число треугольника Паскаля равно сумме предыдущей диагонали, стоящей над этим числом.
-
Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число.
-
Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.
-
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
-
Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше.
-
Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные - в белый, то образуется треугольник Серпинского.
-
Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры.